Division Definition, Symbol, Examples
The division is a strategy to conveying a method of distributing things into two halves. It is one of the four basic operations of arithmetic, which gives a fair result of sharing.
The division is an operation inverse of multiplication. If 3 groups of 4 make 12 in multiplication; 12 divided into 3 equal groups give 4 in each group in division.
For instance:
There are 16 balls and 4 boxes, how to place 16 balls into four equivalent measured boxes?

So, 16 divided by 4 =?
Therefore, 4 balls should be kept in each box.
Suppose there are 12 chocolates, and 3 friends want to share them, how do they divide the chocolates?
Answer: They should get 4 each.
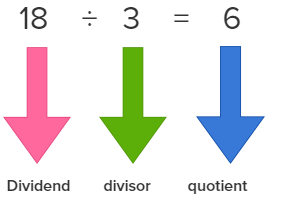
Dividend ÷ divisor = quotient
Dividend : The dividend is the number that is being divided in the division process.
Divisor: The number by which dividend is being divided by is called divisor.
Quotient : A quotient is a result obtained in the division process.
So, in the above process where we divided 16 balls into 4 equal groups;
The dividend is 16, the divisor is 4 and thus the quotient is 4.
Introduction to remainder
The remainder is the portion of the dividend that is left over after division. For example, on dividing 83 by 2, there is a leftover of 1.
It means, 83 ÷ 2 = 41 and r =1,
Here, ‘r’ is remainder.
Fun facts about division
· When dividing something by 1, the answer will always be the original number. It means if the divisor is 1, the quotient will always be equal to the dividend such as 10 ÷ 1= 10.
· Division by 0 is undefined.
· The division of the same dividend and divisor is always 1. For example: 4 ÷ 4 = 1.
Long division method
Long Division Method is the most well-known strategy used to take care of issues on division. In this process, the divisor is written outside the right parenthesis, while the dividend is placed within. The remainder is composed over the overbar on top of the profit. The quotient in mathematics can be defined as the result of the division between a number and any divisor. It is the occasions the divisor is contained in the profit without the rest of negative.
Stage 1: Take the principal digit of the profit. On the off chance that this digit is more greater than or equivalent to the divisor.
Stage 2: Then divide it by the divisor and compose the appropriate response on top.
Stage 3: Subtract the outcome from the digit and compose beneath.
Stage 4: Again, repeat a similar cycle.
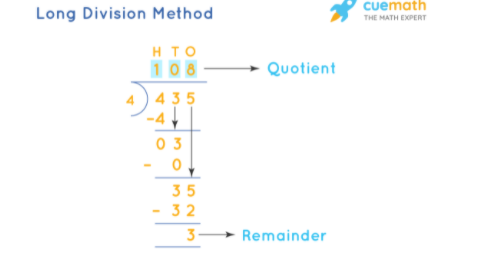
Let us understand the process of division with the help of an example. For example, we are to divide 435 by 4. Hence, we need 435 ÷ 4.
Here, the first digit is 4 and it is equal to the divisor. So, 4 ÷ 4 =1; 1 is written on top. The result 4 × 1 =4 is subtracted from the digit and 0 is written below.
Next drop the second digit or the digit in the ten’s place beside 0. Since 03 is less than 4, we cannot divide this number. Hence, we write a 0 on the top and drop the digit on the unit place beside 3.
Now, we have 35. As 35 > 4, we can divide this number and write 35 ÷ 4 = 8 on top.
Subtract the result 4 × 8 = 32 from 35 and write 3.
3 is known as the remainder and 108 is called the quotient.
Examples on division of integers on different types of questions on integers are discussed here step by step.
**1. Divide 91 by 7
Solution:**
91 ÷ 7
= 91/7
=13
· **2. Divide -117 by 13
Solution:**
-117 ÷ 13
= -117/13
= -9
**3. Divide -98 by -14
Solution:**
-98 ÷ (-14)
= -98/-14
= 98/14
= 7
**4. Divide 324 by -27
Solution:**
324 ÷ (-27)
= - 324/27
= -12
**5. Find the quotient of (-1728) ÷ 12
Solution:**
(-1728) ÷ 12
= - 1728/12
= -144
6. **Find the value of [32 + 2 x 17 + (-6)] ÷ 15
Solution:**
[32 + 2 x 17 + (-6)] ÷ 15
= [32 + 34 + (-6)] ÷ 15
= (66 - 6) ÷ 15
= 60 ÷ 15
= 60/15
= 4
| 7. **Find the value of | -17 | + 17 | ÷ | -25 | - 42 |
Solution:**
| -17 | + 17 | ÷ | -25 | - 42 |
| = | 17 + 17 | ÷ | 25 – 42 |
| = | 34 | ÷ | -17 |
= 34 ÷ 17
= 34/17
= 2
8. Simplify: {36 ÷ (-9)} ÷ {(-24) ÷ 6}
Solution:
{36 ÷ (-9)} ÷ {(-24) ÷ 6}
= {36/-9} ÷ {-24/6}
= - (36/9) ÷ - (24/6)
= (-4) ÷ (-4)
= -4/-4
= 4/4
Binary division – rules and examples
The binary division activity is like the base 10 decimal framework, aside from the base 2. The division is presumably quite possibly the most difficult tasks of the essential number-crunching activities. There are various approaches to take care of division issues utilizing twofold tasks. Long division is one of them and the simplest and the most effective way.
Binary division rules
The binary division is much easier than the decimal division when you remember the following division rules. The main rules of the binary division include:
- 1÷1 = 1
- 1÷0 = Meaningless
- 0÷1 = 0
- 0÷0 = Meaningless
Similar to the decimal number system, the binary division is similar, which follows the four-step process:
- Divide
- Multiply
- Subtract
- Bring down
Examples
Solve 01111100 ÷ 0010
Solution:
Given
01111100 ÷ 0010
Here the dividend is 01111100, and the divisor is 0010
Remove the zero’s in the Most Significant Bit in both the dividend and divisor, that doesn’t change the value of the number.
So the dividend becomes 1111100, and the divisor becomes 10.
Now, use the long division method.

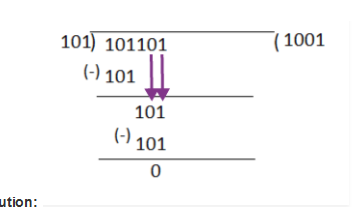
2.Solve using the long division method: 101101 ÷ 101
Using synthetic division to divide polynomials
Synthetic division is a shorthand method of dividing polynomials for the special case of dividing by a linear factor whose leading coefficient is 1.
To explain the process, let us look at the following example
Divide 2x3−3x2+4x+52x3−3x2+4x+5 by x+2x+2 using the long division algorithm.

Simpler version
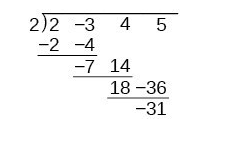
Synthetic division : conveys this simplification even a couple of more advances. Breakdown the table by moving every one of the lines up to fill any empty spots. Likewise, rather than separating by 2, as we would in division of entire numbers, and afterward duplicating and deducting the center item, we change the indication of the “divisor” to – 2, increase, and add. The interaction begins by cutting down the main coefficient.

Synthetic division is a shortcut that can be used when the divisor is a binomial in the form x – k. In synthetic division, only the coefficients are used in the division process.
Using synthetic division to divide when you have two polynomials
1. Write k for the divisor.
2. Write the coefficients of the dividend.1. Bring the leading coefficient down.
2. Multiply the leading coefficient by k. Write the product in the next column.
3. Add the terms of the second column.
4. Multiply the result by k. Write the product in the next column.
5. Repeat steps 5 and 6 for the remaining columns.
6. Use the bottom numbers to write the quotient. The number in the last column is the remainder and has degree 0, the next number from the right has degree 1, the next number from the right has degree 2, and so on.
Using synthetic division to divide Second Degree Polynomial
5x2−3x−365x2−3x−36 by x−3x−3.

Just as with long division, we can check our work by multiplying the quotient by the divisor and adding the remainder.
(x−3)(5x+12)+0=5x2−3x−36
Using synthetic division method to divide a third-degree polynomial

The graph of the polynomial function f(x)=4x3+10x2−6x−20f(x)=4x3+10x2−6x−20 shows a zero at x=−2x=−2. This confirms that x+2x+2 is a factor of 4x3+10x2−6x−204x3+10x2−6x−20.
Using synthetic division method to divide a fourth-degree polynomial
Use synthetic division to divide −9x4+10x3+7x2−6−9x4+10x3+7x2−6 by x−1x−1.

The result is −9x3+x2+8x+8+2x−1−9x3+x2+8x+8+2x−1.
Example of repetition problem
In my living room, there are 120 books in total, placed on 6 shelves. Knowing that each shelf has the same number of books, calculate how many books there are on each shelf.
In order to solve this problem, we must think: if there are 120 books in total, spread equally on 6 shelves, to determine how many books there are on each shelf we divide 120 by 6.
On a trip through the woods, we picked 80 blackberries, which we used completely making cakes. If we put 4 blackberries in each cake, how many blackberry cakes did we make?
We must think: if we arrange all of the blackberries in groups of 4 across all the cakes, by dividing the 80 blackberries by the 4 that go in each cake, we will obtain the number of cakes.
Comparison problem
From NYC, a bus going to Louis’ town costs $12, which is 3 times more than it costs to go to Martha’s town. How much does the bus cost to go to Martha’s town?
In order to solve the problem, we must think: If it costs three times the amount to go to Louis’ town than to Martha’s town, that is to say, that to Martha’s town, it will cost 3 times less. As a result, we will divide 12 ÷ 3 to get the cost to Martha’s town.
Paul is a bus driver. He told me that every trip he takes is 240 miles and that he travels at an average speed of 60 miles per hour. How long does it take to complete his journey?
In order to solve the problem, we must think: if he maintains a speed of 60 miles per hour, it is to say that every hour that he drives, he covers 60 miles. Also, we know that in total he covers 240 miles. Therefore, in order to know the time it will take, we must divide 240 by 60: His journey lasts 4 hours.
‘



