HCF Definition with examples
Highest Common Factor
The Highest Common Factor(HCF) of two numbers is the highest possible number that divides both the numbers precisely. HCF of an and b is meant by HCF(a, b). Let d be the HCF(a, b), then you can’t find the common factor of a and b greater than the number d. The highest common factor (HCF) is also called the greatest common divisor (GCD).
There is more than one technique to discover the HCF of two numbers. Probably the speediest approaches to discover the HCF of two numbers is to utilize use the prime factorization of each number and afterwards the result of minimal forces of the normal prime factors will be the HCF of those numbers. Investigate the universe of HCF by going through its different viewpoints and properties. Discover answers to questions like what is the most elevated regular factor for a gathering of numbers, simple approaches to computing HCF, its connection with LCM, and find additional intriguing realities around them.
Definition of HCF
For a better comprehension of the ideas of LCM (Lowest Common Multiple) and HCF (Highest Common Factor), we need to remember the terms products and elements. We should find out about LCM, HCF, and connection among HCF and LCM of characteristic numbers.
The least or smallest common multiple of any two or more given natural numbers are termed LCM. For example, the LCM of 10, 15, and 20 is 60.
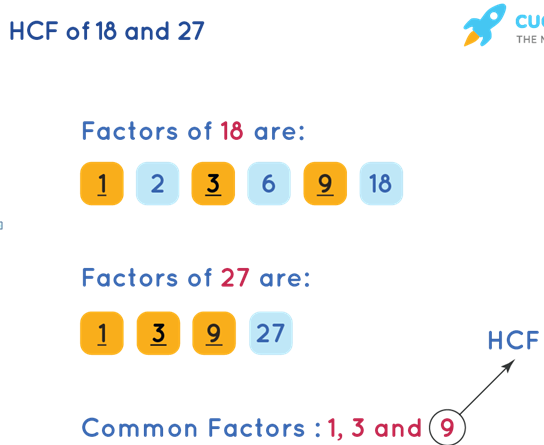
The HCF (Highest Common Factor) of at least two numbers is the highest number among every one of the common factors of the given numbers or in straightforward words, the HCF (Highest Common Factor) of two characteristic numbers x and y is the largest possible number that divides both x and y. We should comprehend this definition utilizing two numbers, 18 and 27. The basic components of 18 and 27 are 1, 3 and 9. Among these numbers, 9 is the highest (largest) number. Along these lines, the HCF of 18 and 27 is 9. This is composed as: HCF (18,27)= 9.
How to find HCF
There are numerous approaches to track down the most elevated normal factor of the given numbers. Independent of the technique the response to the HCF of the numbers would consistently be the same. There are 3 strategies to compute the HCF of two numbers:
- HCF by listing out the common factors
- HCF by prime factorization
- HCF by division method
Let us to examine every strategy in detail by understanding the models.
HCF by listing out the common factors
In this strategy, we list out the factors of each number and determine the common factors of those numbers. At that point, among the common factors, we decide the highest common factor. We should comprehend this strategy utilizing a model.
We will discover the HCF of 30 and42. We will list the components of 30 and 42. The elements of 30 are1, 2, 3, 5, 6, 10, 15, and 30 and the variables of42 are1, 2, 3, 6, 7, 14, 21, and 42. Unmistakably, 1, 2, 3, and 6 are the common factors of 30 and 42. But,6 is the common factor and the greater one. Henceforth, the HCF of 30 and 42 is 6.
HCF by prime factorization
In this technique, we track down the prime factorization of each number and track down the common prime factors of those numbers. At that point, we discover the HCF of those numbers by product of the prime factors that are common to each of the given numbers. How about we comprehend this technique utilizing a model.
We will discover the HCF of 60 and90. How about we address the numbers utilizing the prime factorization.So, we have, 60 = 2 × 2 × 3 × 5 and90 = 2 × 3 × 3 × 5. Now,HCF of 60 and 90 the result of basic prime factors, are, 2, 3, and 5. Thus, HCF of 60 and 90 =2 × 3× 5 = 30.
HCF by division method
In this technique, we divide the bigger number by the smaller number and check the remainder. At that point, we make the rest of the above advance as the divisor and the divisor of the above step as the dividend and perform the long division again. We proceed with the long division measure till we get the rest of 0 and the last divisor will be the HCF of those two numbers. Let’s comprehend this technique utilizing a model.
How about we discover the HCF of 198 and 360 utilizing the division strategy. Among the given two numbers,360 is the bigger number, and198 is the more modest number. We divide 360by 198 and check the rest. Here, the rest of 162. Make the rest of as the divisor and the divisor 198 as the profit and play out the long division once more. We will proceed with this interaction till we get the rest of 0 and the last divisor will is 18 which is the HCF of 198 and 360.
HCF by listing out the common factors
In this method, we have noted down the components of each number and decide the common factors of those numbers. At that point, among the normal components, we decide the highest common factor. How about we comprehend this strategy utilizing a model. We will discover the HCF of 30 and 42. We will list the variables of 30 and 42. The variables of 30 are 1, 2, 3, 5, 6, 10, 15, and 30 and the elements of42 are 1, 2, 3, 6, 7, 14, 21, and 42. Unmistakably, 1, 2, 3, and 6 are the regular components of 30 and 42. But,6 is the normal factor and the best one. Subsequently, the HCF of 30 and 42 is 6.
Properties of HCF
Presently, you definitely realize that the HCF of an and b is the highest common factor of the numbers a and b. Allow us to have a glance at the significant properties of HCF.
The properties of HCF are given below.
HCF of at least two numbers divides every one of the numbers without a remainder.
HCF of at least two numbers is a factor of every one of the numbers.
HCF of at least two numbers is in every case not exactly or equivalent to every one of the numbers.
HCF of at least two indivisible numbers is 1 always.
Examples of HCF
Using the above definition, the HCF of:
· 60 and 40 is 20, i.e, HCF(60,40) = 20
· 100 and 150 is 50, i.e, HCF(150,50) = 50
· 144 and 24 is 24, i.e, HCF(144,24) = 24
· 17 and 89 is 1, i.e, HCF(17,89) = 1
2.The product of LCM and HCF of any two given natural numbers is equivalent to the product of the given numbers.
LCM × HCF = Product of the Numbers
Suppose A and B are two numbers, then.
LCM (A & B) × HCF (A & B) = A × B
Example : If 3 and 8 are two numbers.
LCM (3,8) = 24
HCF (3,8) = 1
LCM (3,8) x HCF (3,8) = 24 x 1 = 24
Also, 3 x 8 = 24
Proved.
3.HCF of co-prime numbers is 1. Thus, LCM of given co-prime numbers is equivalent to the product of the numbers.
Let us take two coprime numbers, such as 21 and 22.
LCM of 21 and 22 = 462
Product of 21 and 22 = 462
LCM (21, 22) = 21 x 22
4. H.C.F. and L.C.M. of Fractions:
LCM of fractions = LCMofnumeratorsHCFofdenominators
HCF of fractions = HCFofnumeratorsLCMofdenominators
Let us take two fractions 4/9 and 6/21.
4 and 6 are the numerators & 9 and 12 are the denominators
LCM (4, 6) = 12
HCF (4, 6) = 2
LCM (9, 21) = 63
HCF (9, 21) = 3
According to the formulae, LCM (4/9, 6/21) = 12/3 = 4
HCF (4/9, 6/21) = 2/63
5. HCF of any two or more numbers is never greater than any of the given numbers.
Example: HCF of 4 and 8 is 4
Here, one number is 4 itself and another number 8 is greater than HCF (4, 8), i.e.,4.
6. Prove that: LCM (9 & 12) × HCF (9 & 12) = Product of 9 and 12
9 = 3 × 3 = 3²
12 = 2 × 2 × 3 = 2² × 3
LCM of 9 and 12 = 2² × 3² = 4 × 9 = 36
HCF of 9 and 12 = 3
LCM (9 & 12) × HCF (9 & 12) = 36 × 3 = 108
Product of 9 and 12 = 9 × 12 = 108
Hence, LCM (9 & 12) × HCF (9 & 12) = 9 × 12 = 108.
7. Find the highest common factor (H.C.F) of 15 (Fifteen) and 35 (Thirty five).
Factors of 15 (Fifteen) = 1, 3, 5 and 15.
Factors of 35 (Thirty five) = 1, 5, 7 and 35.
Therefore, common factor of 15 (Fifteen) and 35 (Thirty five) = 1 and 5.
Highest common factor (H.C.F) of 15 (Fifteen) and 35 (Thirty five) = 5.
8. Find the highest common factor (H.C.F) of 21 (Twenty one) and 35 (Thirty five).
Factors of 21 (Twenty one) = 1, 3, 7and 21.
Factors of 35 (Thirty five) = 1, 5, 7 and 35.
Therefore, common factor of 21 (Twenty one) and 35 (Thirty five) = 1 and 7.
Highest common factor (H.C.F) of 21 (Twenty one) and 35 (Thirty five) = 7.
9. Find the highest common factor (H.C.F) of 30 (Thirty) and 24 (Twenty four).
Factors of 30 (Thirty) = 1, 2, 3, 5, 6, 10, 15 and 30.
Factors of 24 (Twenty four) = 1, 2, 3, 4, 6, 8, 12 and 24.
Therefore, common factor of 30 (Thirty) and 24 (Twenty four = 1, 2, 3, and 6.
Highest common factor (H.C.F) of 30 (Thirty) and 24 (Twenty four = 6.
10. Find the highest common factor (H.C.F) of 33 (Thirty three) and 55 (Fifty five).
Factors of 33 (Thirty three) = 1, 3, 11 and 33.
Factors of 55 (Fifty five) = 1, 5, 11 and 55.
Therefore, common factor of 33 (Thirty three) and 55 (Fifty five) = 1 and 11.
Highest common factor (H.C.F) of 33 (Thirty three) and 55 (Fifty five) = 11.
11. 8 and 9 are two co-prime numbers. Using these numbers verify, LCM of Co-prime Numbers = Product Of The Numbers.
LCM and HCF of 8 and 9:
8 = 2 × 2 × 2 = 2³
9 = 3 × 3 = 3²
LCM of 8 and 9 = 2³ × 3² = 8 × 9 = 72
HCF of 8 and 9 = 1
Product of 8 and 9 = 8 × 9 = 72
Hence, LCM of co-prime numbers = Product of the numbers.
12. Find the HCF of 1225, 910, 1835, 2140.
12 = 2 × 2 × 3
9 = 3 × 3
18 = 2 × 3 × 3
21 = 3 × 7
HCF (12, 9, 18, 21) = 3
25 = 5 × 5
10 = 2 × 5
35 = 5 × 7
40 = 2 × 2 × 2 × 5
LCM(25, 10, 35, 40) = 5 × 5 × 2 × 2 × 2 × 7 = 1400
The required HCF = HCF(12, 9, 18, 21)/LCM(25, 10, 35, 40) = 3/1400
13. Two numbers are in the ratio of 5:11. If their HCF is 7, find the numbers.
Solution: Let the numbers be 5m and 11m. Since 5:11 is already the reduced ratio, ‘m’ has to be the HCF. So, the numbers are 5 x 7 = 35 and 11 x 7 = 77.
14. Find the length of the plank which can be used to measure exactly the lengths 4 m 50 cm, 9 m 90 cm and 16 m 20 cm in the least time.
Solution : Let us first convert each length to cm. So, the lengths are 450 cm, 990 cm and 1620 cm. Now, we need to find the length of the largest plank that can be used to measure these lengths as the largest plank will take the least time. For this, we need to take the HCF of 450, 990 and 1620.
450 = 2 x 3 x 3 x 5 x 5 = 2 x 32 x 52
990 = 2 x 3 x 3 x 5 x 11 = 2 x 32 x 5 x 11
1620 = 2 x 2 x 3 x 3 x 3 x 3 x 5 = 22 x 34 x 5
Therefore, HCF (450, 990, 1620) = 2 x 3 x 3 x 5 = 90
Thus, we need a plank of length 90 cm to measure the given lengths in the least time.
15. Find the largest number which divides 64, 136 and 238 to leave the same remainder in each case.
Solution : To find the required number, we need to find the HCF of (136-64), (238-136) and (238-64), i.e., HCF (72, 102, 174).
72 = 23 x 32
102 = 2 x 3 x 17
174 = 2 x 3 x 29
Therefore, HCF (72, 102, 174) = 2 x 3 = 6
hence, 6 is the required number.



