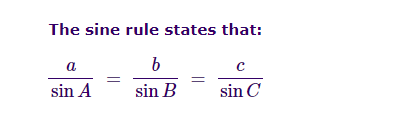Triangle Definition, Area, Perimeter, Height all Formulas
Definition of Triangle
A triangle is a three-sided polygon that closes in a space. It utilizes lines, line sections or beams (in any mix) to shape the three sides. At the point when three sides structure and meet, they make three vertices or corners.
The corners inside the triangle are inside points. The corners outside the triangle are outside points. “Triangle” in a real sense implies three points, “tri” is a Latin prefix for three, similar to tricycle (three wheels), trio (three individuals from a gathering), or rear arm muscles (three muscles in a gathering).
Properties of Triangle
· A triangle has three sides, three vertices, and three angles.
· The sum of the three interior angles of a triangle is always 180°.
· The sum of the length of two sides of a triangle is always greater than the length of the third side.
· A triangle with vertices P, Q, and R is denoted as △PQR.
· The area of a triangle is equal to half of the product of its base and height.
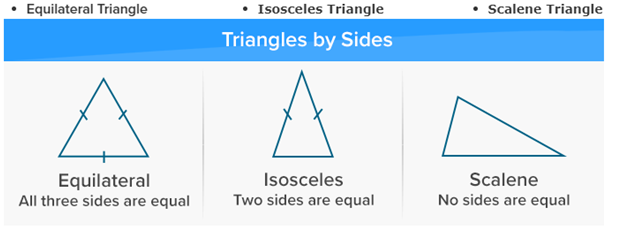
Types of Triangle
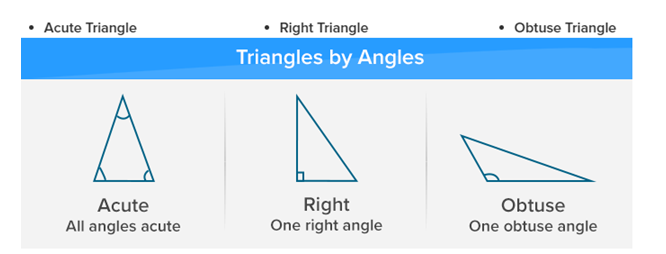
An intense triangle has all inside points intense (under 90°), a correct triangle has one right point (equivalent to 90°) and an uncaring triangle has one harsh point (more prominent than 90°).
Here we have a rough version of Eastern State Penitentiary’s mighty wall. It is 20 feet tall and forms one of the two sides of the right triangle. The prisoners’ escape ladder was 30 feet tall and forms the leaning hypotenuse. The distance from the wall to the ladder is the base of our triangle. Our right triangle is named △ESP△ESP. It has three sides:
1. ESES – 20 feet (the wall)
2. SPSP – 22.36 feet (distance from the bottom of the wall to the ladder’s feet)
3. PEPE – 30 feet (the hypotenuse; the ladder itself)
It has three angles:
1. ∠E∠E, an acute angle measuring around 41°41°
2. ∠S∠S, a right angle, measuring exactly 90°90°
3. ∠P∠P, another acute angle measuring around 48°L
Base of a Triangle
Each side of a triangle can be its base. You single out the base just when you are wanting to develop an elevation, or tallness, for your triangle. As a rule, the base is introduced on a level plane to you, yet that isn’t required. Any place the elevation is built, the side it meets is the base.
Altitude of a Triangle
Recall the getting away from detainees’ inclining stepping ladder? The mass of the jail was the stature; the stepping stool was the hypotenuse, which is longer than the correct triangle’s tallness. The tallness or elevation of a triangle is found by developing an opposite line from one side of a triangle to the contrary point.
In a correct triangle, you have two instant elevations, the different sides that are not the hypotenuse.
Remember the getting away from detainees’ inclining stepping stool? The mass of the jail was the tallness; the stepping stool was the hypotenuse, which is longer than the correct triangle’s stature. The stature or elevation of a triangle is found by developing an opposite line from one side of a triangle to the contrary point.
In a correct triangle, you have two instant heights, the different sides that are not the hypotenuse.
In △ESP△ESP, side ESES is the altitude for the way the triangle looks now. If we turn the entire picture 90°90°, side SPSP is now the altitude. If we turned the triangle around so the hypotenuse (the ladder side) was horizontal, we could construct an altitude from that hypotenuse up to ∠S∠S. We would find that altitude to be 14.91 feet in height.
We would discover that elevation to be 14.91 feet in tallness. The elevation, or stature, is consistently opposed to the base and consistently meets the contrary point. Each triangle has three elevations. Just in a symmetrical triangle will every one of the three elevations be compatible.
The elevation, or tallness, is consistently opposed to the base and consistently crosses the contrary point. Each triangle has three heights. Just in a symmetrical triangle will each of the three heights be consistent.
Opposite angle
Each side has its opposite angle. The hypotenuse, PEPE, has an opposite ∠S∠S; side ESES has the opposite ∠P∠P, and side SPSP has the opposite ∠E∠E.
This also means every angle has an opposite side. ∠S∠S has opposite side PEPE, the hypotenuse, and so on.
Adjacent sides
Pick any side of the triangle. The two sides touching it are adjacent, which means they are touching. So for side PEPE, sides ESES and SPSP are adjacent.
Pick any angle of the triangle. The two sides forming it are its adjacent sides. So for ∠E∠E, sides ESES and PEPE are adjacent.
Formulae of Triangle area
In general, the term “area” is defined as the region occupied inside the boundary of a flat object or figure. The estimation is done in square units with the standard unit being square meters (m2). For the calculation of region, there are pre-characterized equations for squares, square shapes, circle, triangles, and so forth In this article, we will gain proficiency with the space of triangle equations for various sorts of triangles, alongside some model issues.
The space of a triangle is characterized as the complete district that is encased by the three sides of a specific triangle. Fundamentally, it is equivalent to half of the base occasions tallness, for example A = 1/2 × b × h. Thus, to discover the space of a tri-sided polygon, we need to know the base (b) and tallness (h) of it. It is material to a wide range of triangles, regardless of whether it is scalene, isosceles or symmetrical. To be noticed, the base and tallness of the triangle are opposite to one another. The unit of the 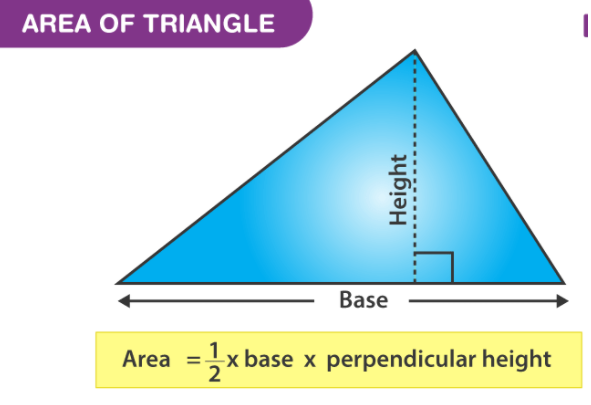 the region is estimated in square units (m2, cm2).
the region is estimated in square units (m2, cm2).
Example: What is the area of a triangle with base b = 3 cm and height h = 4 cm?
Using the formula,
Area of a Triangle, A = 1/2 × b × h = 1/2 × 4 cm × 3 cm = 2 cm × 3 cm = 6 cm2
Aside from the above formula, we have Heron’s equation to figure the triangle’s region, when we know the length of its three sides. Additionally, trigonometric functions are utilized to find the area when we know two sides and the angle formed between them in a triangle. We will calculate the area for all the conditions given here.
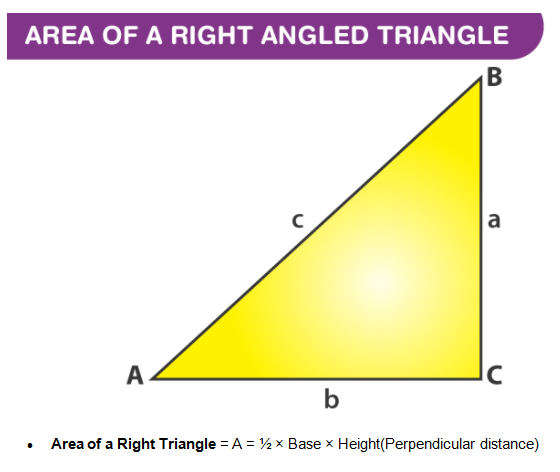
Finding the Area of a Right-angled Triangle
A right-angled triangle, also called a right triangle has one angle at 90° and the other two acute angles sums to 90°. Therefore, the height of the triangle will be the length of the perpendicular side.
Finding the Area of an Equilateral Triangle
An equilateral triangle is a triangle where every one of the sides is equivalent. The perpendicular drawn from the vertex of the triangle to the base partitions the base into halves.

- Area of an Equilateral Triangle = A = (√3)/4 × side2
Finding the Area of an Isosceles Triangle
An isosceles triangle has two of its sides equal and also the angles opposite the equal sides are equal.
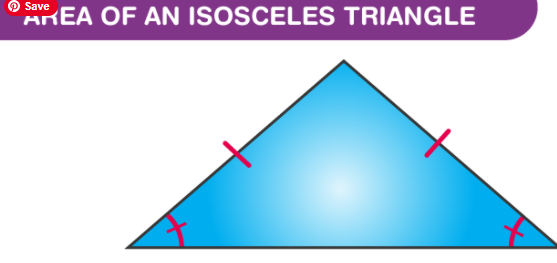
- Area of an Isosceles Triangle = A = ½ (base × height)
Finding the Perimeter of a Triangle
The perimeter of a triangle is the distance covered around the triangle and is determined by adding every one of the three sides of a triangle.
Using Heron’s formula
The space of a triangle with 3 sides of various measures can be discovered utilizing Heron’s formula. Heron’s recipe incorporates two significant advances. The initial step is to track down the semi border of a triangle by adding every one of the three sides of a triangle and partitioning it by 2. The subsequent stage is that, apply the semi-border of triangle esteem in the fundamental recipe called “Heron’s formula” to discover the space of a triangle.
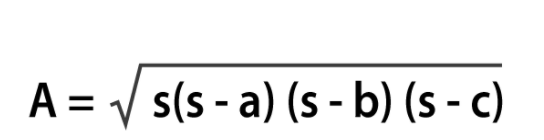
The perimeter of a triangle = P = (a + b + c) units where a, b and c are the sides of the triangle.
Two sides and an included angle
Let us take a triangle ABC, whose vertex angles are ∠A, ∠B, and ∠C, and sides are a,b and c, as shown in the figure below.
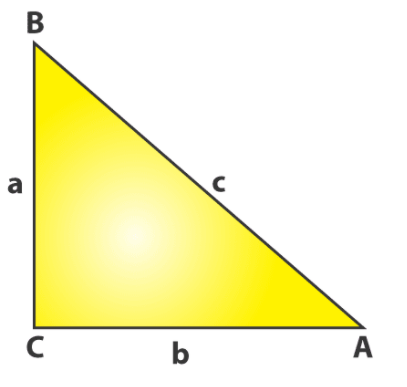
Area (∆ABC) = ½ bc sin A
Area (∆ABC) = ½ ab sin C
Area (∆ABC) = ½ ca sin B
These formulas are very easy to remember and also to calculate.
For example, If, in ∆ABC, A = 30° and b = 2, c = 4 in units. Then the area will be;
Area (∆ABC) = ½ bc sin A= ½ (2) (4) sin 30
= 4 x ½ (since sin 30 = ½)
= 2 sq.unit.
The volume of a triangular prism
A prism that has 3 rectangular appearances and 2 equal three-sided bases, at that point it is a three-sided prism. The three-sided bases are joined by horizontal faces and are corresponding to one another. The space involved by the three-sided prism is the volume of the three-sided prism.
The image beneath shows the three-sided prism which will help in inferring the formula. Let’s solve one example.
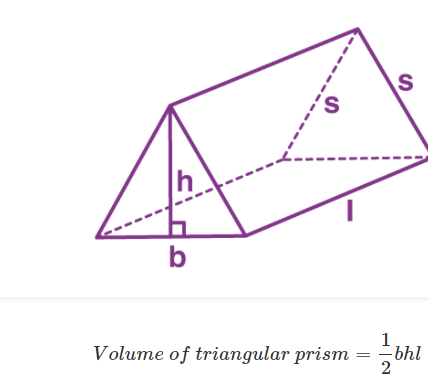
Question. Find out the volume of a triangular prism with the base of altitude 4 cm, side 3 cm and height of the prism is 6 cm
Solution:
Given,
b = 3 cm
h = 4 cm
l = 6 cm
According to the formula,
The volume of triangular rprism=12blh
=12×3×4×6
=36cm3
Height of a Triangle in 3 Different Situations
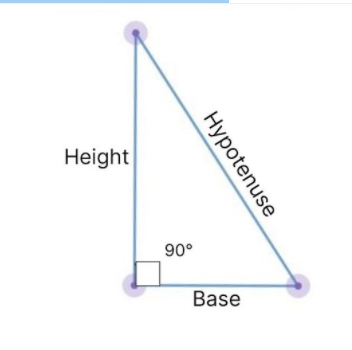
Right-angled Triangle
A right angled triangle has three sides: the hypotenuse, stature, and base of the triangle. The base and height of a right triangle are consistently the sides adjacent to the right angle, and the hypotenuse is the longest side.
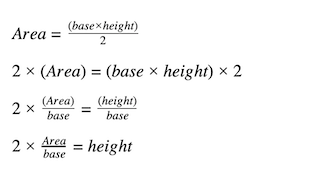
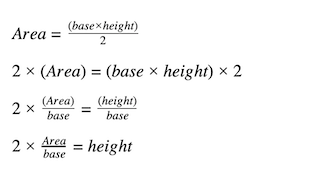
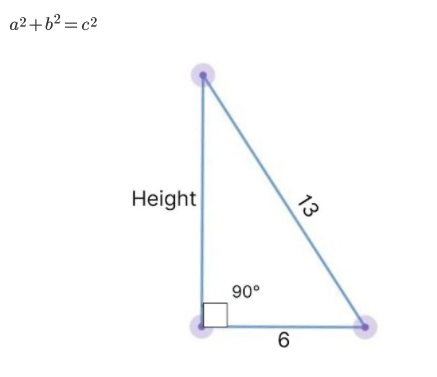
If the given area isn’t known, you can use the Pythagorean theorem to solve for the height of a right triangle. Here’s what the Pythagorean theorem states, given C is the hypotenuse and a and b are the other two sides:
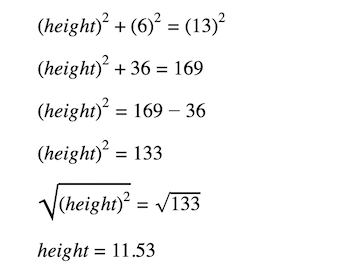
Height of a Non-Right Triangle

Unfortunately, you can’t use the Pythagorean theorem to find the height of an isosceles triangle or the height of an equilateral triangle.
You’ll have to use Heron’s formula to solve for the area of the entire triangle.
The first step of Heron’s formula is calculating half the triangle’s perimeter. In this case, s represents half the perimeter and a, b, and c are the sides:
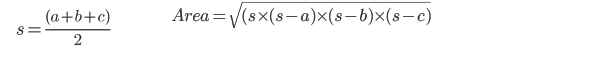

Question : 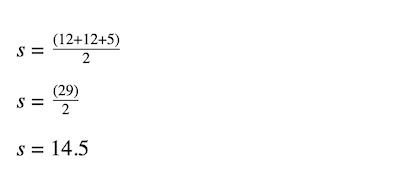
Using Area To Find the Height of a Triangle

Geometry formula triangle
The angles in a triangle add up to 180°.
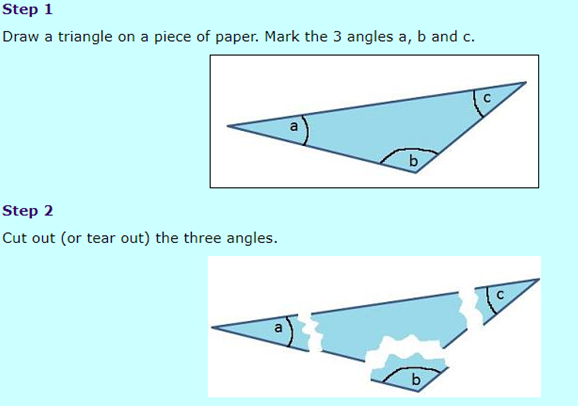
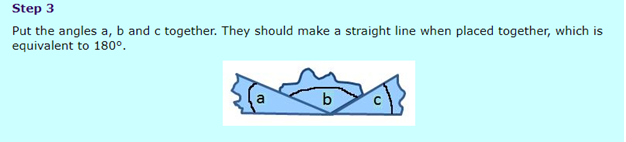
Find the missing angle in the triangle below.
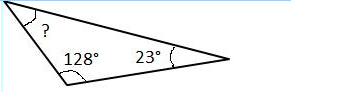
So we know that ? + 128 + 23 = 180.
This means that ? = 180 - 128 - 23 = 29°.
So the missing angle is 29°.
Pythagoras’ Theorem
Pythagoras’ hypothesis expresses that in a correct triangle (or right-calculated triangle) the amount of the squares of the two more modest sides of the triangle is equivalent to the square of the hypotenuse.
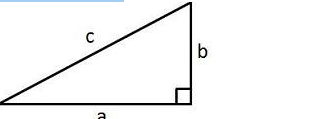
where c is the hypotenuse (the longest side) and a and b are the other sides of the right triangle.
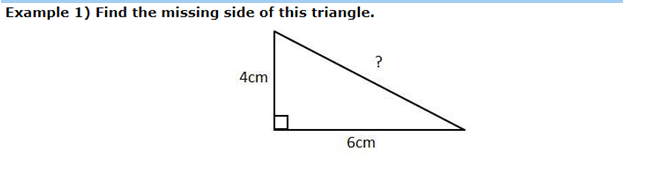
In this model, we need to discover the hypotenuse (longest side of a correct triangle).
So utilizing Pythagoras, the amount of the two more modest squares is equivalent to the square of the hypotenuse.
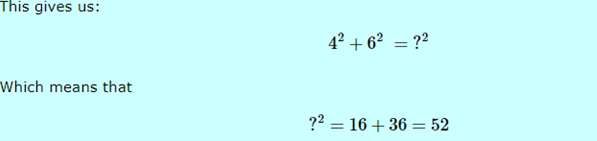
Basic triangle trigonometry
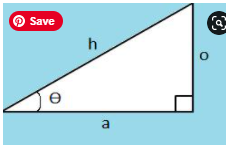
Allow us to begin by naming the pieces of this triangle.
θ is one of the points of the correct triangle (however not the correct point!)
h is the hypotenuse - the longest side of the correct triangle
o is inverse to the point
a is neighbouring the point

Sine and Cosine
The fundamental triangle geometry equations above will just work for right triangles - they won’t work for triangles without right points.
The accompanying formulas underneath will work for any triangle.
Once more, in the event that we start with the naming of the sides and points of the triangle:
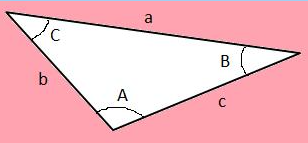
a is the side opposite angle A;
b is the side opposite angle B;
c is the side opposite angle C.