Fraction Addition, Multiplication, Division and Subtraction

Definition of fraction

Fractions address equivalent pieces of an entire or an assortment.

Fraction of a whole: When we partition an entire into two halves, each part is a fraction of the whole.

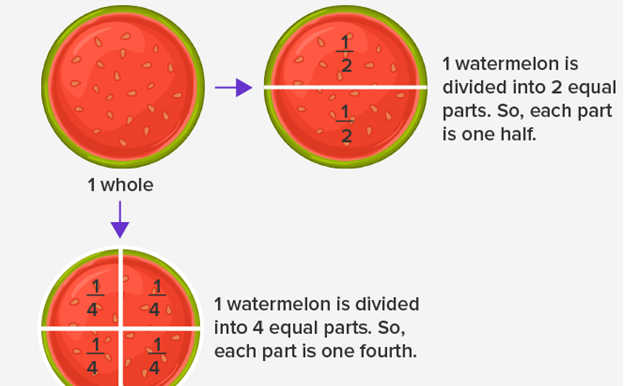
There are total of 5 children.

3 out of 5 are girls. So, the fraction of girls is three-fifths ( 3⁄5 ).

2 out of 5 are boys. So, the fraction of boys is two-fifths ( 2⁄5 ).

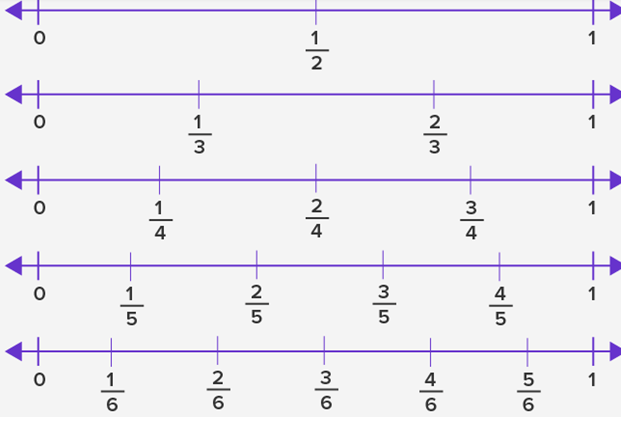
Fractions on a number line

Examples

The most common examples of fractions from real life are equal slices of pizza, fruit, cake, a bar of chocolate, etc.

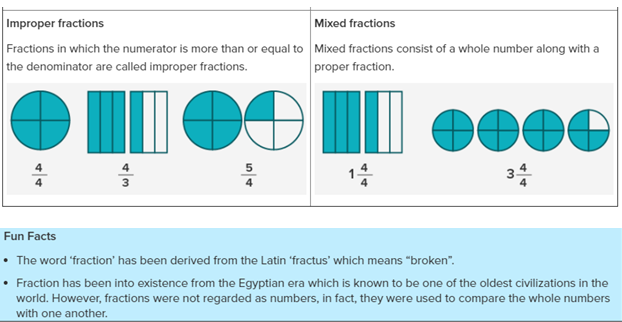
Types of fractions

Addition of fractions

Addition of fractions depends on two major conditions:

Same denominators

Different denominators

Denominators are same, such divisions are supposed to resemble parts and can be added straightforwardly. Be that as it may, assuming the denominators are extraordinary, (such divisions are called not normal for portions) we need to defend the denominators and afterward add the numerators, keeping the denominators of the parts normal. Learn like or dissimilar to divisions, here.

Adding fractions with different denominators

We have effectively figured out how to add two portions when the denominators resemble or same. Here we will examine, how to add the portions when the denominators are dissimilar to or unique.

To add two divisions, whose denominators are extraordinary, we need to legitimize the denominator first, by taking the LCM. Presently we need to increase portions, numerator and denominator so that the denominators of the two divisions become equivalent to the LCM esteem.

After the denominators have gotten equivalent, we can add the numerators, keeping the denominator normal.

We should comprehend it with a model:

3/12 + 5/2

Solution: Let us write the fraction into the more simplified form:

¼ + 5/2

Now, we can see here the denominators of the two fractions are different, i.e. 4 and 2.

Step 1: Rationalise the denominator by taking the LCM

LCM of 4 and 2 = 2

Step 2: Multiply and divide the second fraction by 2, to make its denominator equal to 4

5/2 x (2/2) = 10/4

Step 3: Since the denominator is same for both the fractions, therefore we can add them:

¼ + 10/4

Step 4: Add the numerator, keeping the denominator common.

(1+10)/4

= 11/4

Therefore, the addition of 3/12 + 5/2 is 11/4.

Adding fractions with whole numbers

It is easier to add fractions with whole numbers than it is to add fractions with mixed numbers. Let’s look at an example and see what I mean. If the denominator of both numbers is the same, we use it as the general denominator and add the numerators. To demonstrate how to add fractions with whole numbers, such as a/b and c/b, we will take the following steps.

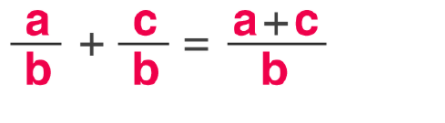
The denominator of both fractions, b, is the same.

Keeping b as the denominator, apply the numerators.

The sum of all fractions would yield the resulting.

Fractions with Co-prime Denominators

Co-prime denominators: Denominators that have no universal variables other than 1.

Let’s look at how to combine co-prime variables.

Procedure:

To find the denominator of the resulting fraction, multiply the denominator.

To find the numerator, multiply the numerator of one fraction by the denominator of the other.

Now, include the outcome.

Adding Mixed Fractions

Let’s understand how to add mixed fractions with an example:

Example: Add : 3 ⅓ + 1 ¾

10/3 + 7/4 = [(10 × 4) / (3 × 4)] + [(7 × 3) /(4 × 3)] = (40 / 12) + (21 / 12) = 61 / 12

Subtraction of Fractions

As we all know, addition and subtraction are mathematical operations that are very similar. Furthermore, we add two or more numbers, while subtraction subtracts one number from another. As a result, fraction subtraction follows the same law as fraction addition.

If the denominators of two fractions are the same, we will explicitly subtract the numerator while retaining the denominator the same.

If the denominators of fractions are different, we need to rationalise them first and then perform subtraction.

Some examples are:

Example 1: Subtract ⅓ from 8/3.

Solution: We need to find,

8/3 – ⅓ = ?

Since the denominator of two fractions ⅓ and 8/3 is common, therefore, we can directly subtract them:

8/3 – ⅓ = (8-1)/3 = 7/3

Example 2: Subtract ½ from ¾.

Solution: We need to subtract ½ from ¾, i.e.,

¾ – ½ = ?

Since the denominators of two fractions are different, therefore, we need to rationalise them by taking the LCM.

LCM (4,2) = 4

Now multiply the ½ by 2/2, to get 2/4

Therefore,

¾ – 2/4 = (3-2)/4 = ¼

Hence, ¾ – ½ = ¼

Multiplication of Fractions

The multiplication of fractions begins with the numerators being multiplied, followed by the denominators being multiplied. The resulting fraction is then generalised further and, if necessary, reduced to its simplest terms.

To help you recall the steps outlined above, there is an amusing rhyme. “It’s not difficult to multiply fractions; top times top over bottom times bottom. And don’t hesitate to simplify before saying good-by.” With that, let us proceed to learn more about fraction multiplication.

Multiplication of fractions is not the same as addition or subtraction of fractions, where the denominator and numerator would be the same. Any two fractions with opposite denominators can be easily multiplied here. The only thing to remember is that the fractions should not be mixed; they should be either proper or improper fractions. Let’s practise multiplying fractions:

Multiply the numerators.

Multiply the denominators.

Reduce the resultant fraction to its lowest terms.

For example, let’s multiply the following fractions: 2/3 × 4/5. We start by multiplying the numerators: 2 × 4 = 8, then, the denominators: 3 × 5 = 15. This can be written as: (2 × 4)/(3 × 5) = 8/15. Now, the product is already in its lowest terms, so we need not reduce it and we give this as the answer.

Visual representation of multiplication

Visualizing fractional multiplication with fractional squares is an intriguing way to grasp the idea. Can you get what fractional squares are? Fractional squares are square representations of given fractions, with the numerator indicated as the shaded part. Let’s take a look at how to multiply a fraction with fractional squares. Let’s add these two fractions together 2/3 × 1/2.

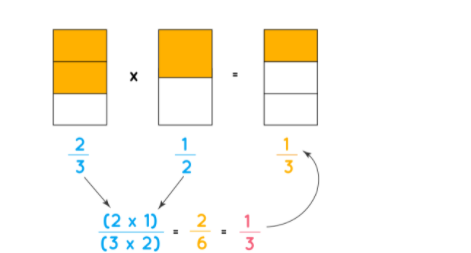The fractional square on the left in the diagram above has two orange-shaded portions instead of three equal sections. Two-thirds of the fractional square is represented by this orange field. Similarly, the shaded field in the second row represents half of the fraction rectangle. We get 2/6 by combining these two fraction squares. This can be expressed by one element of three squares in its simplest form. Thus, 2/3 × 1/2 = 2/6 = 1/3. Now that you have the insight into multiplying fractions, let us explore this topic further.

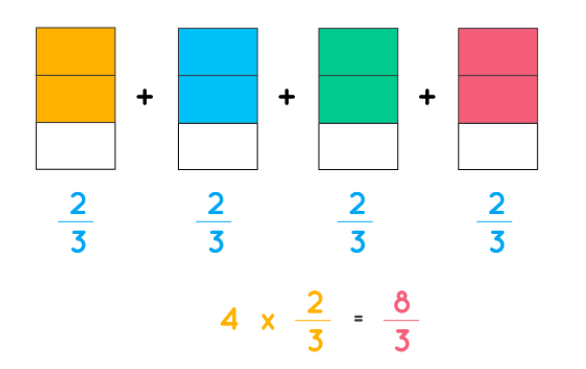
The definition of multiplying fractions by whole numbers is simple. Consider the following example: 4 and a half. We’ll start by representing this example with fractional squares. The formula for four times two-thirds is:

Now let us change the improper fraction obtained into a mixed fraction. 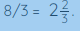Multiplication of proper fractions is the easiest of all. For example, let us take 2/3 × 4/6. Here, 2/3 and 4/6 are proper fractions. To multiply them, we will take the following steps:

We will multiply the numerators together: 2 × 4 = 8.

Then multiply the denominators together: 3 × 6 = 18. This can also be written as: (2 × 4)/(3 × 6) = 8/18.

Then, reduce the resultant fraction to its lowest terms which will be 4/9.whole and two thirds which is equal to 8/3. Finally, we get the following representation.

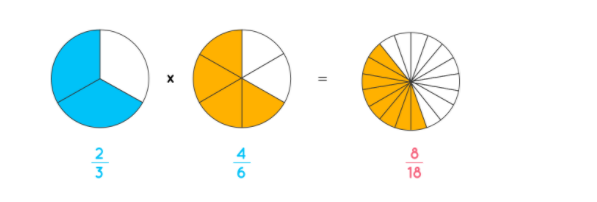
Multiplication of improper fractions

We do assume that an incorrect fraction has a numerator that is greater than the denominator. We frequently get an improper fraction when we multiply two improper fractions. For example, to multiply 3/2 7/5, which are both improper fractions, we must do the following:

Multiply the denominators and numerators.

(3 7) / (2 5) = 21/10

Hence, the answer is: 21/10 which can be written as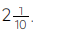

Mixed fractions are fractions that have a whole number and a fraction, like When multiplying mixed fractions, we need to change the mixed fractions into an improper fraction before multiplying. For example, if the number is 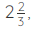you should change this to (3 × 2 + 2)/3 = 8/3. Let’s consider an example. To multiply Change the given mixed fractions to improper fraction. (8/3) × (13/4)

Multiply the numerators of the improper fractions, and then multiply the denominators. This will give 104/12.

Now, reduce the resultant fraction to its lowest terms, which will make it 26/3.

Further, convert the answer back to mixed fraction which will be: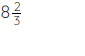

Dividing fractions

.When you divide a fraction, you are wondering how many classes of the divisor (second number) are included in the dividend (first number). In the preceding equation, we are wondering how many 16 exist in 12.

Consider the example equation to be a cake. You only have half of the cake. How many servings of cake do you have left if each serving is one-sixth of the total?

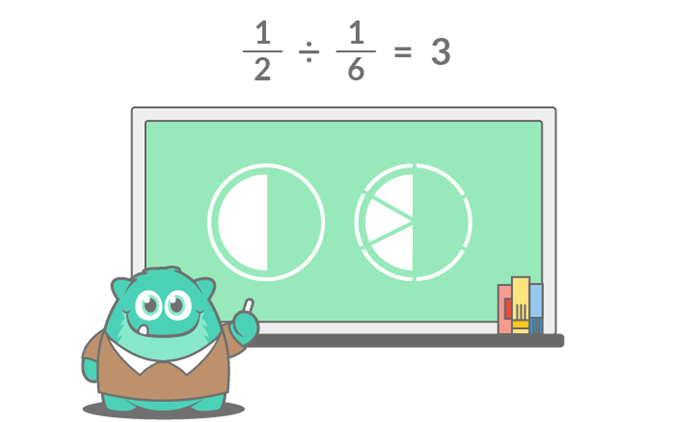
How to divide fractions

If you just divided fractions like you were dividing a regular math puzzle, you’d most likely get some complex fractions and something like this:

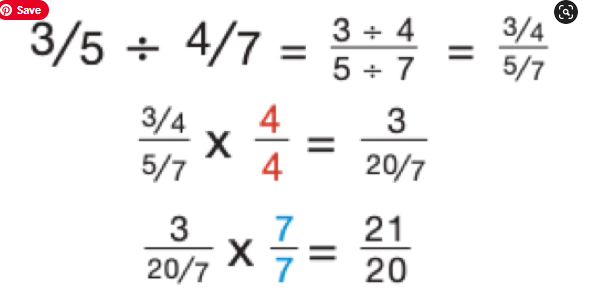
The following three steps should be used to solve the majority of division problems:

Convert the divisor to a reciprocal.

Multiply by changing the division sign to a multiplication symbol.

If at all necessary, simplify your answer.

Examples of dividing fractions

An improper fraction is one in which the numerator is greater than the denominator. The appearance of these fractions may be perplexing, but the sequence of operations remains constant.

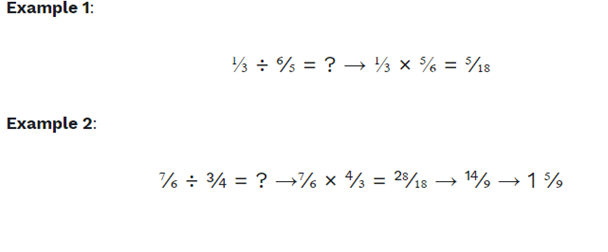
Dividing mixed fractions

When you have a whole number and a percentage, you have a combined fraction. 2 ½ will be called a mixed fraction, for example. What is the best way to split a mixed fraction?

Proceed with the three-step technique after converting the mixed fraction to an inappropriate fraction. To do so, multiply the total by the denominator. Then take the value and multiply it by the numerator.

2 ½ changes to ⁵⁄₂.

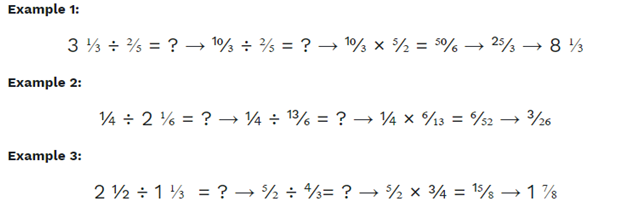
Whole number fraction division

Make the numerator a whole number and the denominator one to convert a whole number to a fraction.

3 → ³⁄₁

After converting the entire amount to a fraction, you can proceed with the three-step technique to solve the dilemma.

Fraction to percent

When comparing amounts, we usually use fractions and percentages. Percentage or percent refers to percentages of a total, while percent refers to how much of the whole lot is left and is easier to recall than a percentage.

Consider the following example to better explain the principle of fraction and percentage: suppose a class has 38 students, 23 of whom are female. What is the proportion of female students now?It is 23 out of 38. To simplify: 23/38 = 0.60526315789473684210526315789474 or about 60%.

What exactly is Percent?

The word percent refers to a ratio or an amount expressed as a fraction of 100. It is represented by the percentage symbol percent. Here’s an analogy to help you understand how the hundred reflects a fraction of 100. In fractional form, 35% is written as 35/100. In class, 50 percent of the students were male, which suggests that 50 students out of every 100 were male.

Formulae

A percentage is a number or ratio whose denominator is equal to 100. The percentage formula is given as follows:

For example, if we want to find 10% of 150, it can be done as:

(10/ 100) × 150 = 1500/ 100

= 15

Converting fraction into percentage

To convert a fraction to a percentage, simply multiply it by 100 and divide the result by 100. Here are a few explanations to help you learn how to transform a fraction to a percentage. Take the steps below to transform a fraction to a percentage:

Convert the fraction to decimal form.

To get a percent value, multiply the received decimal number by 100.

Thus, 10% of 150 is 15.

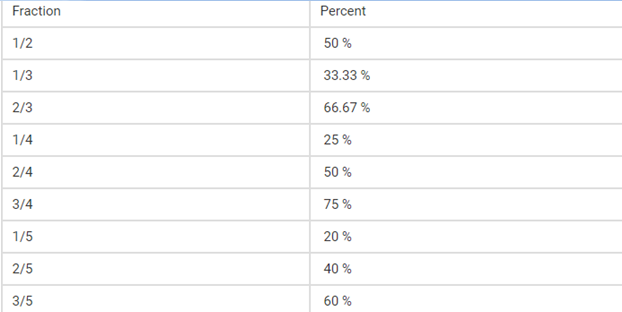Examples of Fraction to Percent

Example 1: Convert 3/4 to a percent.

Solution:

Step 1: Convert the fraction 3/4 into decimal

Step 2: 3/4 = 0.75

Example 2: Convert 3/16 to percent.

Solution:

Step 1: Convert the fraction 3/16 into decimal

Step 2: 3/16 =0.1875

Step 3: Multiply the decimal by 100: 0.1875 × 100 = 18.75%

Therefore, the solution is 18.75 %.Step 3: Multiply the decimal by 100: 0.75 × 100 = 75%

Therefore, the solution is 75%.